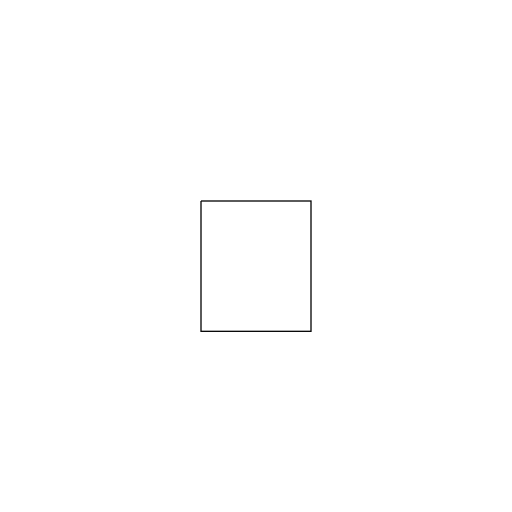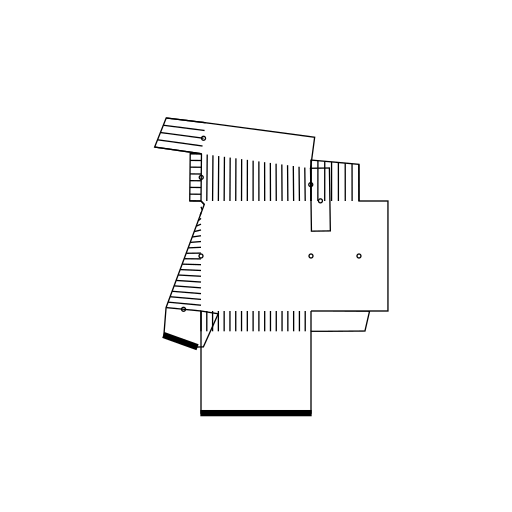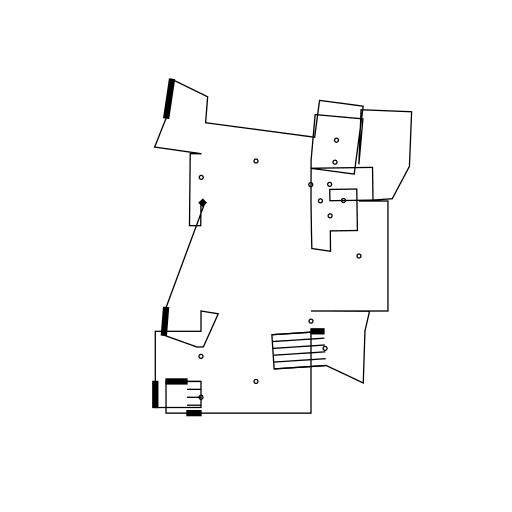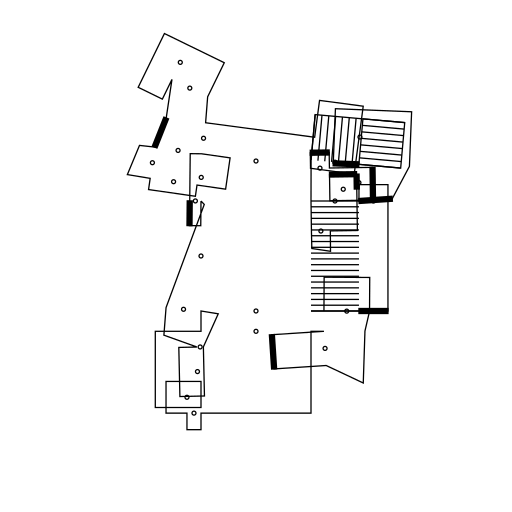I recently made a js version of this, you can see it here.
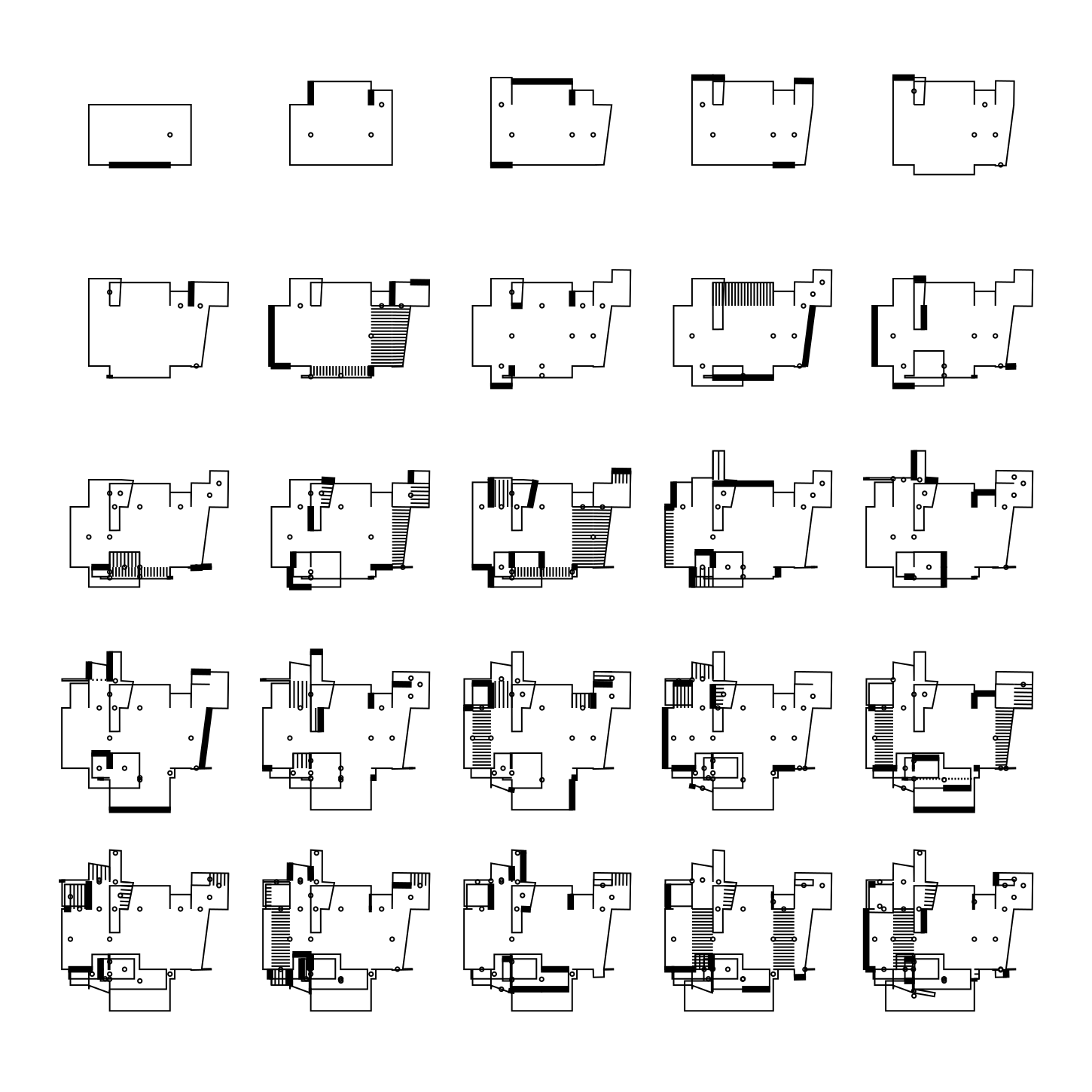
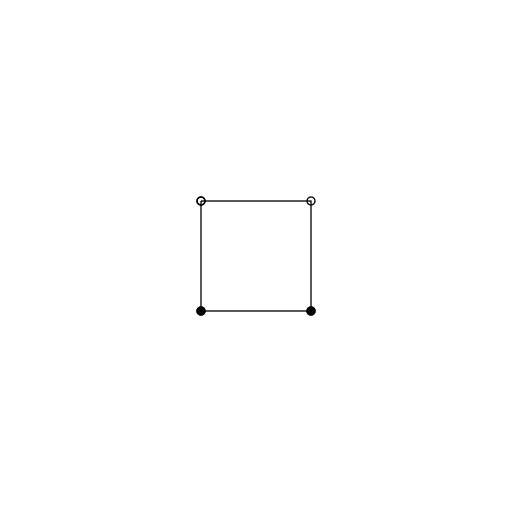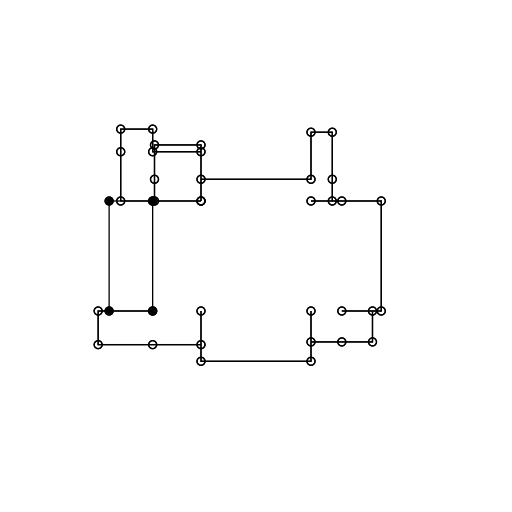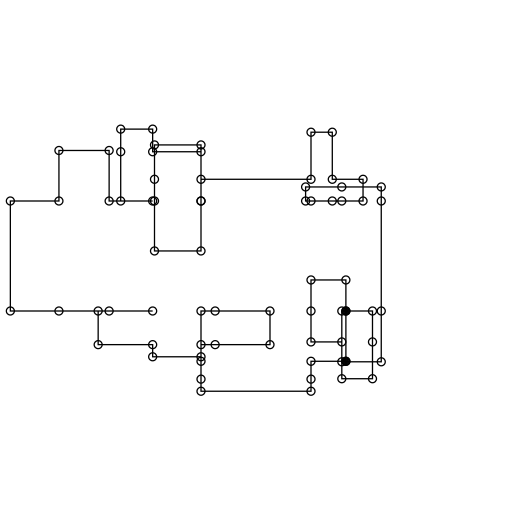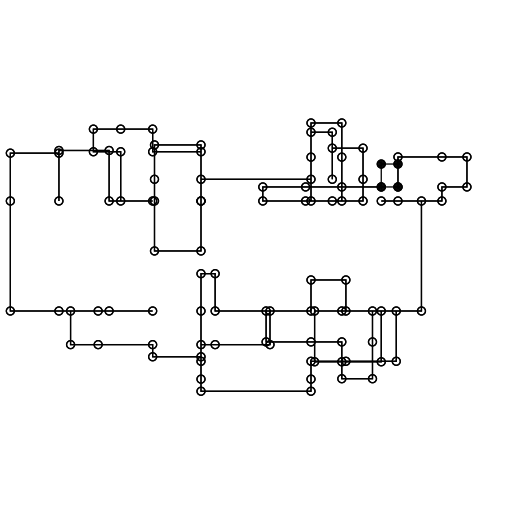
When I published the previous batch of plots I promised I would describe some of the methods I used. So here is a guide to a simple method of generating impossible architecture.
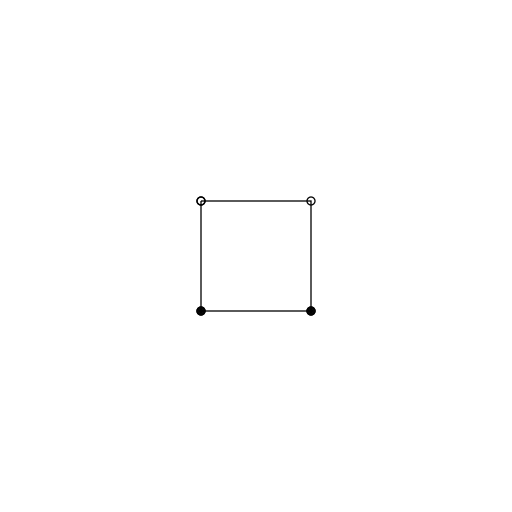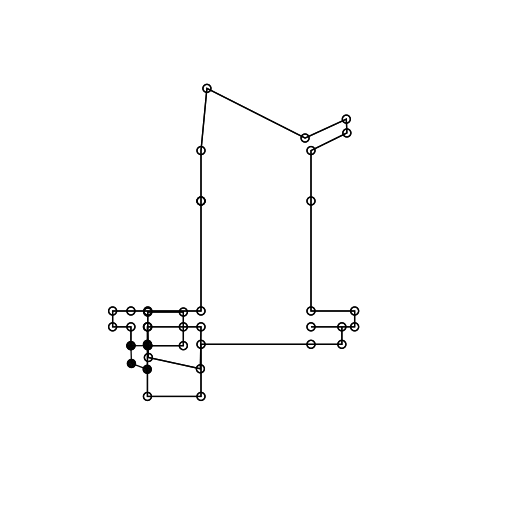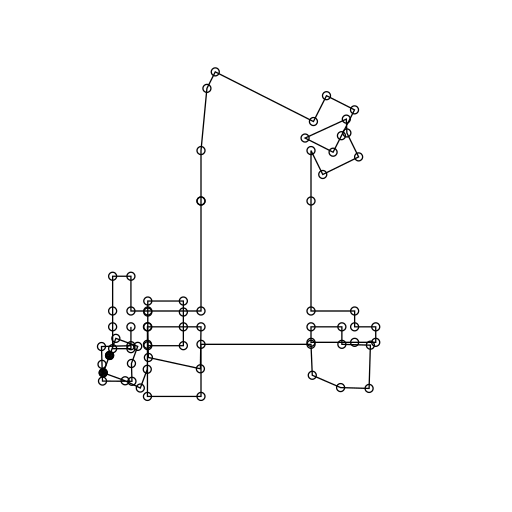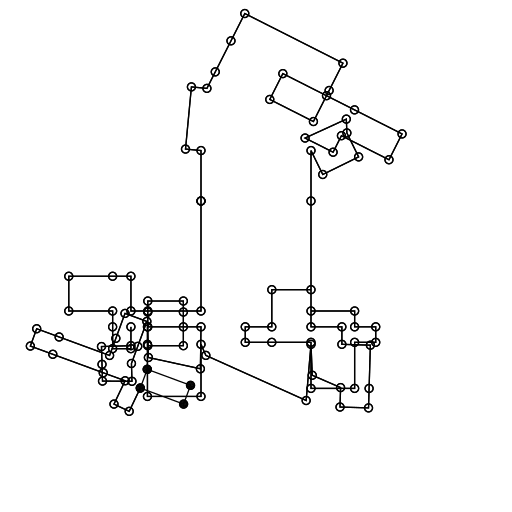
The method relies on recursive extrusions. Let's assume we start with a square. First we randomly select one of the four line segments that make up the square. Then we extrude that edge outwards a certain amount. This has the effect of adding three new line segments. At the same time we remove the line segment that we extruded from. Next we select a new line segment at random, then repeat the process.
To make things a little more interesting you can add various kinds of small tweaks. One tweak I've found to work very well is to occasionally rotate the extruded edge a little. This quickly creates more interesting shapes, without creating too much chaos. Below is a new animation where there is a 20 % chance that the extruded edge will be rotated.
On top of this it is possible to add several other more or less cosmetic tweaks. You will have to figure out this on your own, but below is an example.
There are a lot of possible things to add to make these drawings more believable. The most obvious candidates are doors and windows. Then you could add walls of various widths, and so forth. Having said that: I'm not really that interested in creating believable drawings. The aspect that is fascinating to me is what it takes for you to recognise something as an architectural drawing, when it obviously isn't one.
Initially I was not going to allow the structure to grow "into" itself. However, I quickly realised that self-intersection resulted in interesting structures. For this reason I haven't added any collision tests. However, I think a possible extension is to only allow a certain percentage of intersecting extrusions. That way you can avoid some of the inevitable clutter that happens as you let the structure grow for a long time.
Below is an animation where we keep going long enough for the drawing to delve into chaos.
- When you start doing this you will probably realize that you need to know what the "outside" of your shape is. One possible strategy is make sure that your points are ordered anti-clockwise when you start. Then you can consistently find the outward normal by adding π/2 to the angle corresponding to your line segment.
- Strictly speaking they are not really structures. The algorithm is completely unaware of the spatial aspects of the resulting drawing.