When working with generative algorithms it is convenient to
store the results as you make them. I usually export vector drawings to
.svg. This has a few drawbacks.
Most notably that the actual graph
(topology) is more or less lost in the .svg file. Making it
impossible to re-draw an .svg from the graph with modified drawing
logic.
I have exported results in different ways over time. Among others to .obj files. The following is the most recent attempt to store results in a more convenient way.
In this post I described my Datalog query language for querying graphs in an in-memory graph data structure (cl-grph). You may want to read that post before moving on. However, the following Datalog examples are pretty simple.
Exporting the Graph
Let's make a graph instance, g, with some random data as an
example:
; create a new instance of g, and generate; some random edges with different properties(let ((g (grph:make))) (grph:modify! (g) (loop repeat 20 do (rnd:prob 0.4; -> adds edge between two random; verts with property :pth(-> (rnd:rndi 5) (rnd:rndi 5) (list :pth)); <> add edges in both directions with ; several props: :pth :pth2, (rndprop 10)(<> (rnd:rndi 5) (rnd:rndi 5) (list :pth :pth2 (rndprop 10))))))
The various edge properties like :pth, :pth2, can be
used (among other things) to associate different drawing styles with a set of
edges. Further on we use :stipple for stippled edges.
Here is the query to get all combinations of edges and properties we want to export from our graph:
(grph:qry g :select (?p ?x ?y) :where (?x ?p ?y))
;;
;; :PTH[0-9] are the random properties
;; ((:PTH 0 1) (:PTH 0 3) (:PTH 0 4) (:PTH 1 0) (:PTH 1 4)
;; (:PTH 2 3) (:PTH 3 2) (:PTH 3 4) (:PTH 4 0) (:PTH 4 1)
;; (:PTH 4 2) (:PTH 4 3) (:PTH2 0 1) (:PTH2 0 4) (:PTH2 1 0)
;; (:PTH2 1 4) (:PTH2 2 3) (:PTH2 3 2) (:PTH2 3 4) (:PTH2 4 0)
;; (:PTH2 4 1) (:PTH2 4 3) (:PTH0 0 1) (:PTH0 1 0) (:PTH0 1 4)
;; (:PTH0 4 1) (:PTH2 2 3) (:PTH2 3 2) (:PTH3 0 1) (:PTH3 1 0)
;; (:PTH6 0 1) (:PTH6 1 0) (:PTH8 0 4) (:PTH8 4 0) (:PTH9 3 4)
;; (:PTH9 4 3))
Variables in the cl-grph Datalog implementation have to be
prefixed with ?. So this query can be read as "select all
existing combinations of (?p ?x ?y), where there is an
edge from ?x to ?y, with property ?p".
You no doubt see that the properties are repeated a lot. A more space efficient export can be achieved using this query instead:
(grph:qry g :select (?p (grp ?x ?y)); group (?x ?y) for every ?p:where (?x ?p ?y); same condition as before:collect (list ?p (flatten (grp ?x ?y)))) ;; ;; ((:PTH (4 3 4 2 4 1 4 0 3 4 3 2 2 3 1 4 1 0 0 4 0 3 0 1)) ;; (:PTH0 (4 1 1 4 1 0 0 1)) (:PTH3 (1 0 0 1)) (:PTH6 (1 0 0 1)) ;; (:PTH2 (4 3 4 1 4 0 3 4 3 2 2 3 1 4 1 0 0 4 0 1)) ;; (:PTH8 (4 0 0 4)) (:PTH2 (3 2 2 3)) (:PTH9 (4 3 3 4)))
This seems good enough for now. And importing it again is just a matter of reading the data back in, looping over the properties, and adding them to a fresh graph.
Before we export the graph data to file let's look at a different use case for the query language.
Datalog to SVG
While experimenting with the export I decided to make a small DSL for drawing
SVGs directly from Datalog queries. I won't go into the DSL in
detail here, but you can recognize the Datalog queries pretty easily as they
still use the prefixed variables ?x and ?y as we saw
above.
Also notice that the DSL uses .&
as triggers for symbols to be interpreted in a particular way. Much like the
DSL for vector mathematics I described previously.
Here is the code that draws an .svg from Datalog queries,
using the new DSL; exports the graph (and spatial data) to a .grph
file; and stores the literal code used to draw the .svg alongside
the graph data.
; write grph, g, and spatial data, v, to "tmp2"(grph:write-with-script ("tmp2" g v); SVG and PRNG instance(let ((svg (wsvg:make)) (rs (rnd:make 473))); initiate DSL context (macro)(wsvg/grph:selectors (g v svg); select all :path edges(.&ws ?x ?y (?x :path ?y); draw all segments(.&path :sw 1.75 :so 0.85)); select all :stipple edges(.&ws ?x ?y (?x :stipple ?y); draw stippled segments with prob. 0.7(rnd:prob rs 0.7 (.&stip 2f0 1.3 :sw 0.75 :so 0.7))); select all verts with less; than 3 adjacent verts(.&vs ?x (and (or (?x :path ?y) (?y _ ?x)) (% <= (grph:edge-count g ?x) 3)); draw circles with 0.1 prob.(rnd:prob rs 0.1 (.&circ 8f0 :fill :black :so 0.8 :fo 0.8)))) (wsvg:save svg :fn)))); save svg
In other words the exported .grph file now contains the graph (and
spatial) data right next to the logic used to draw it. Including the
pseudorandom number generator
(PRNG) with appropriate state.
Obviously this might get more complicated for more realistic examples. But below
is a screenshot from a complete .grph file for one of the
illustrations in this post, and it should be quite recognizable.
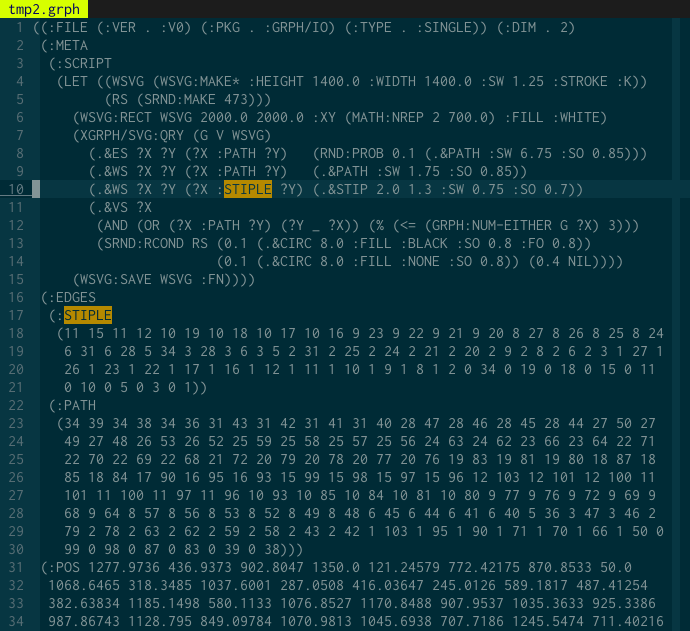
.grph file that contains all the code
neccessary to draw something similar to the other illustrations in this post.
The .grph file is around 4kb, and a corresponding
.svg is around 700kb. Much of the difference in file size is
caused by the stippling, as you might expect
Out of interest I can also point out that the .grph files
for the illustrations in this post are between 10-200 times
smaller than the corresponding .svg. While containing sufficient
information to create the identical .svg again; or draw it in a different
manner.
The utility of this code in particular is pretty marginal to anyone except me. But I hope it serves as an interesting example of how Lisp (macros) can be used to do useful things. Things that—at the very least—would be more cumbersome to achieve in many other languages.
EDIT: In the next post I show how to implement a simplified version of the DSL.
- We will ignore the spatial data in these examples. But it
behaves similarly to a
grphinstance. - Some of the code examples have been simplified, and some function
names have been changed from their implementation in
cl-veqto make things a little more obvious in this context. - Because I have implemented the grp functionality in my Datalog dialect. My version of Datalog is experimental, and probably deviates from any actual Datalog implementation in several ways, this being one of them.
- None of this is to say that
.svgis bad, but it serves a different purpose.