On Generative Algorithms

Sand Spline Github

Sand Spline was an idea I almost discarded because it seemed like it would not yield interesting results. However, I gave it a shot, and I was very pleased with the results almost right away.

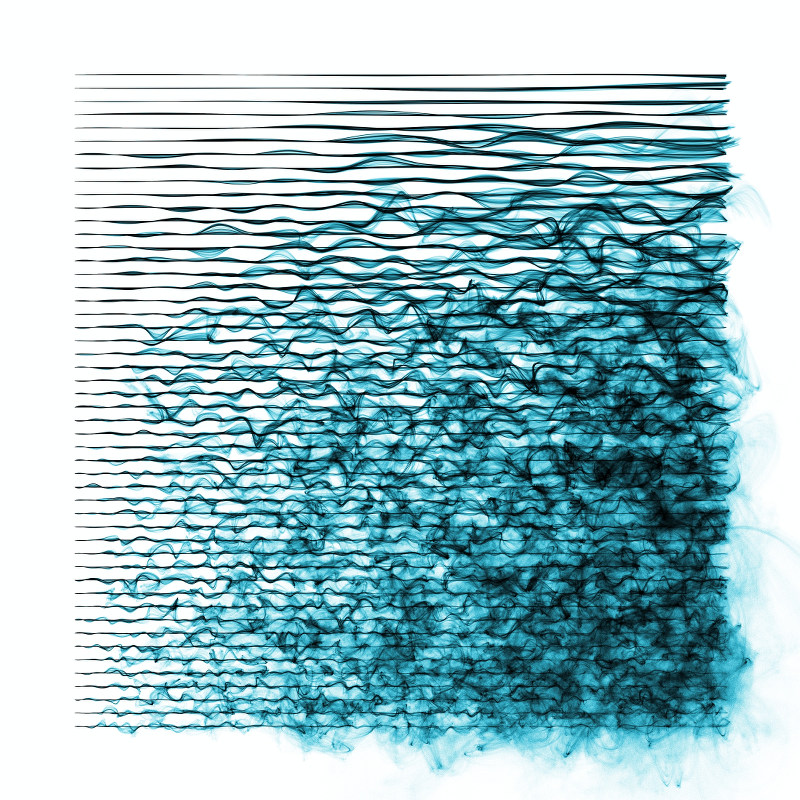
The idea is based on the concept of B-splines. In mathematics a B-spline is a smooth spline that is drawn from a number of nodes (control points) without necessarily passing through the nodes themselves. If you move the nodes a little, the smooth curve will follow along. And if you make the nodes move little by little at random, the spline will gradually become more erratic. You can see this in the animation below.

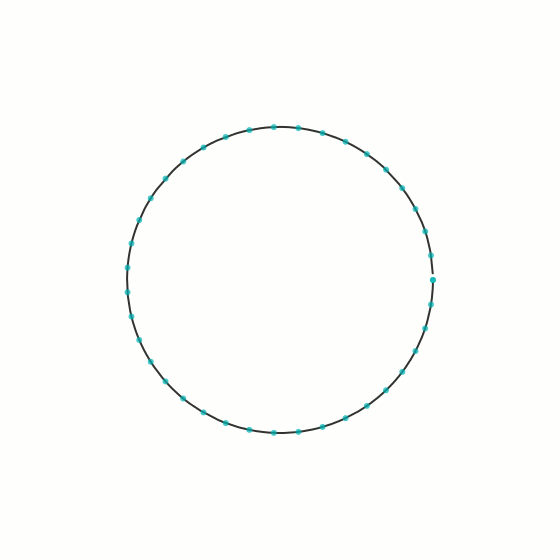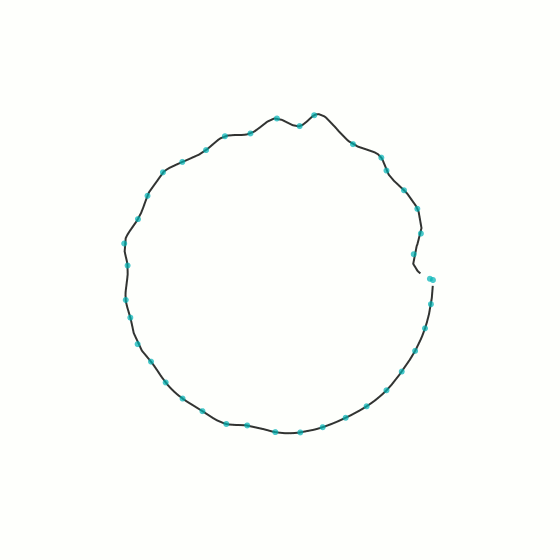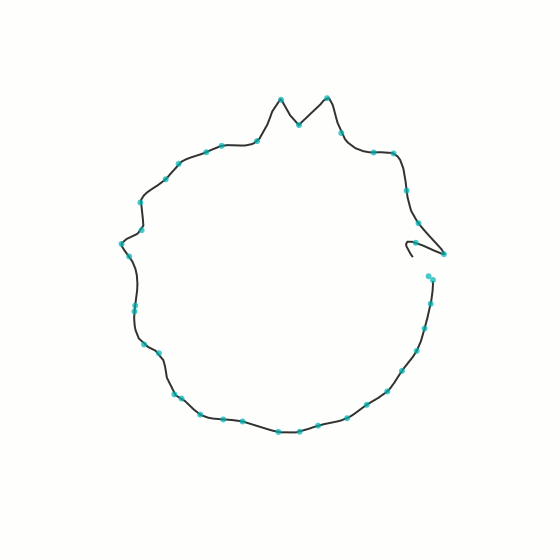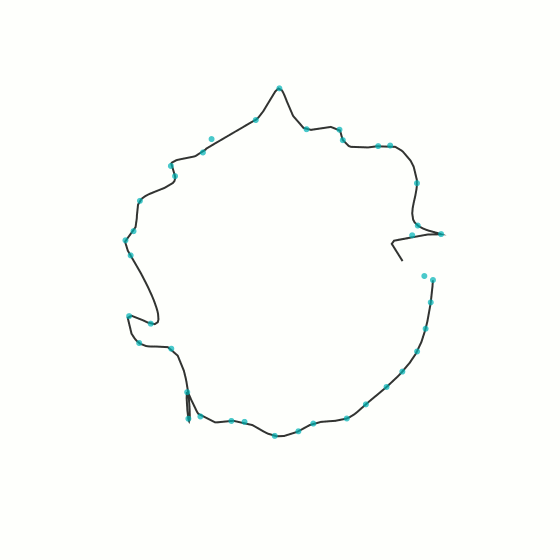
In this animation the spline starts on the right and moves counter-clockwise. You will also notice that the level of noise is larger the further out along the spline we go. This has nothing to do with the spline itself, but it is a nice way to keep the starting node in its original position.

Instead of simply drawing the spline, I draw a series of transparent dots along the spline for every iteration. I also make sure to draw the same number of dots each time, regardless of the length of the spline. Since the movement is gradual, you will get high density where the spline moves slowly, and lower density where the spline moves quickly.

This behaviour, and painting technique, is in many ways similar to several Tarbell works, including Sand Dollar, Limb Sand Stroke, Sand Traveler and Sandstroke. Hence the name. As several people have pointed out to me these images are also very reminiscent of the Lorenz Attractor, even though the method is rather different.

Combining this simple method with different configurations of splines and colours gives a large number of quite different results, and I will probably return to this system to experiment frequently.